為替変動がランダムウォークであるとすると、ある程度長い期間での変化量の分布は正規分布になります。(中心極限定理) この仮定が正しくないことは、長時間足が正規分布でないことから言えそうですが、ここではランダムウォークと為替相場での値動きの大きさを比較します。
次の図は、ユーロドルの1分足のヒストグラムです。2010年1月4日から2020年8月7日のデータを使いました。
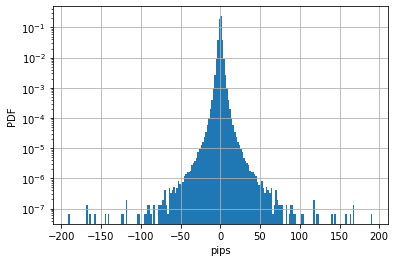
1分あたりの変動の標準偏差を求めると1.94pipsになります。これより、ランダムウォークを仮定すると、1日足の分布は![]() pipsを標準偏差とする正規分布になります。次の図で、この正規分布と実際の1日足の絶対値のヒストグラムを比べてみます。
pipsを標準偏差とする正規分布になります。次の図で、この正規分布と実際の1日足の絶対値のヒストグラムを比べてみます。
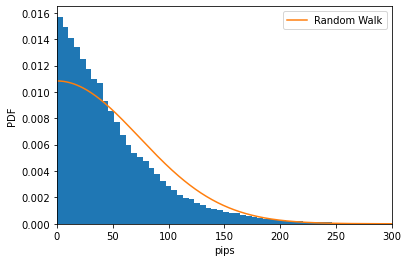
1日足の標準偏差は68.4pipsで、ランダムウォークのそれよりも5.3pips程小さくなっています。つまり、行き過ぎた変動を抑えるような復元力が作用していることが示唆されます。
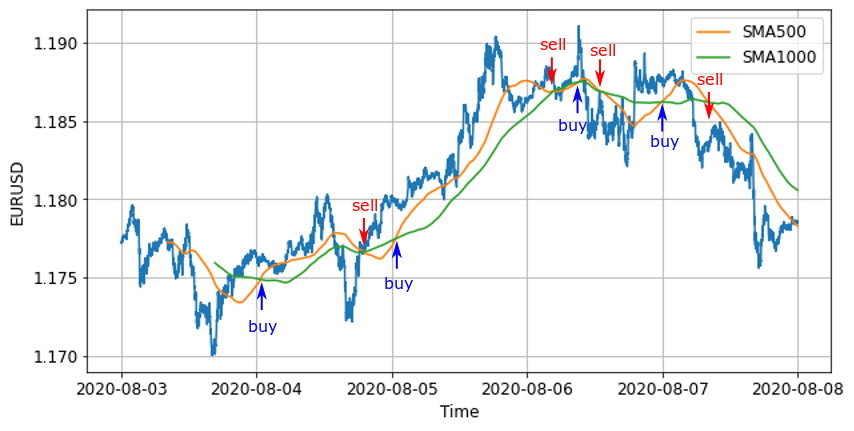
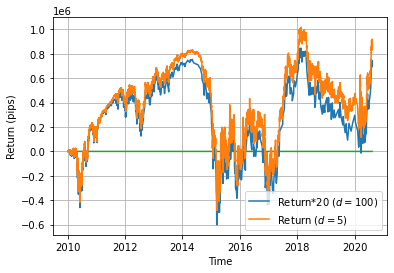
コメント