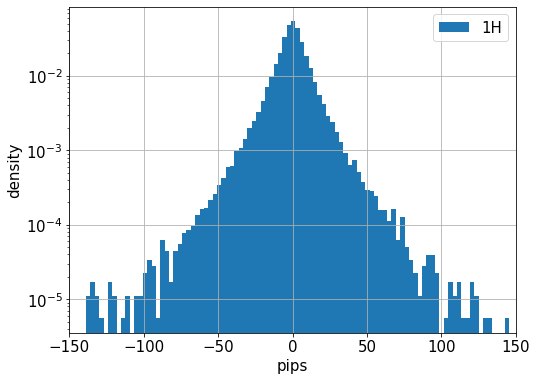
為替変動の確率密度関数は非正規分布で正規分布よりも袖が広いことが知られています。下の図は、EURUSDの過去10年分の1時間足の確率密度関数です。中央付近は指数分布に近く、袖は緩やかな減少になっています。
Kim, Shephard and Chib(1998)による確率的ボラティリティモデルを使って、この確率密度関数を再現するモデル構築を行ってみます。この確率的ボラティリティモデルは、![]() として、
として、
![]()
で表されます。Stanのユーザーガイドにも説明があるモデルです。![]() がリターンで、
がリターンで、![]() が分散を表す潜在変数です。
が分散を表す潜在変数です。![]() は
は![]() に平均的に近づくような正規分布です。Stanを使って、モデルパラメータ
に平均的に近づくような正規分布です。Stanを使って、モデルパラメータ![]() を推定します。Stanの設定はデフォルトのままで、警告なく収束しました。
を推定します。Stanの設定はデフォルトのままで、警告なく収束しました。
次に、これらのパラメータの推定値を使って、リターンの時系列データを生成します。本来は、パラメータ自体もサンプリングされたものですが、ここではStanで得られたサンプル分布の平均値を使います。(![]() は鋭い分布になったので、生成データはほぼ変わらないでしょう。)モデルによって生成されたリターンの確率密度関数を先ほどの図に重ねます。
は鋭い分布になったので、生成データはほぼ変わらないでしょう。)モデルによって生成されたリターンの確率密度関数を先ほどの図に重ねます。
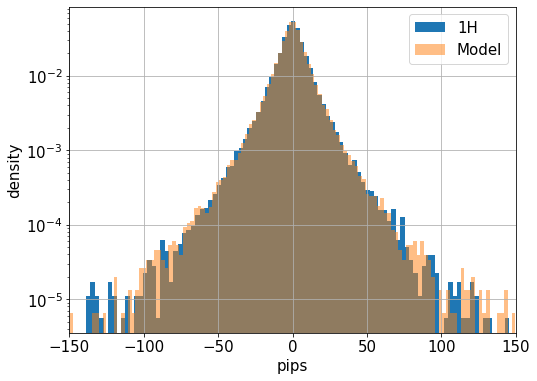
ほぼ一致しています。このような単純なモデルでリターンの確率密度関数を再現するのは驚きです。分散だけに関するものなので将来の価格の予測には使えませんが、変動の大きさを予測することは出来きそうです。将来、この予測の検証を試みたいと思います。また、リターンの分布は時間足に依らず相似で安定分布に近い性質がありますが、このモデルで生成される分布関数が安定分布であるかも知りたい事項です。
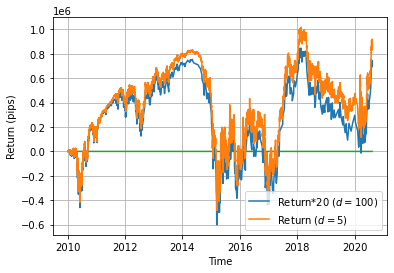

コメント