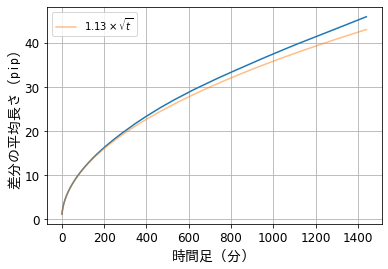
ドル円の分布ではレート自体がどの値を取り易いかを見ました。ここでは、レートの差分の分布を調べてみます。ここでの「レートの差分」とは一定時間間隔でのレート変化のことで、ローソク足の実体部分(ローソク足のヒゲを除いた部分)の長さを指します。まず、この差分の大きさの平均値を様々な時間足(ローソク足)で見てみましょう。次の図は、差分長さの平均値の時間間隔依存性を示しています。例えば、日足(1440分足)では平均長さが約45銭(pip)です。1日毎に方向を予測して、全て的中したときに、平均として45(pip/日)程取れることになります。![]() (
(![]() は横軸座標)に比例したグラフをオレンジ線で表示します。差分の平均長さは
は横軸座標)に比例したグラフをオレンジ線で表示します。差分の平均長さは![]() の変化に良く似ています。特に、短い時間足では両者の変化はほとんど一致してます。これは、統計学で言う再生性という性質に関連しています。例えば、レート変化が確率的ボラティリティモデルに完全に従うと、正規分布の再生性から差分の平均長さは
の変化に良く似ています。特に、短い時間足では両者の変化はほとんど一致してます。これは、統計学で言う再生性という性質に関連しています。例えば、レート変化が確率的ボラティリティモデルに完全に従うと、正規分布の再生性から差分の平均長さは![]() に比例することになります。長めの時間足で、2つのグラフが離れていることから、確率的ボラティリティモデルは完璧なモデルでは無さそうです。
に比例することになります。長めの時間足で、2つのグラフが離れていることから、確率的ボラティリティモデルは完璧なモデルでは無さそうです。
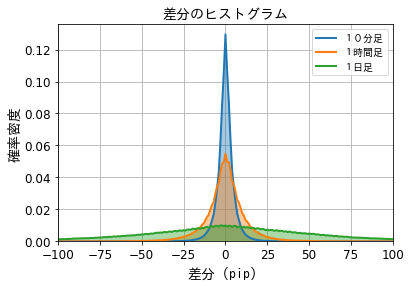
平均値だけではなく、今度は差分長さの分布を調べます。10分、1時間、1日の3つの時間足でのヒストグラムを次の図に示します。時間足が大きいほど、袖の広い平らな分布になります。これは、時間が経つ程、レートが離れたところに位置し易いという感覚から納得出来ます。
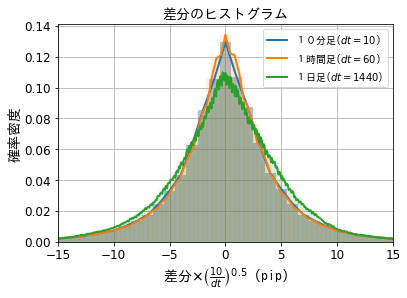
次に、このヒストグラムの横軸の尺度を、時間足に応じて変換します。変換の仕方は、横軸に![]() をかけます。
をかけます。![]() は時間足のことで、1分足、1時間足、1日足はそれぞれ
は時間足のことで、1分足、1時間足、1日足はそれぞれ![]() になります。この横軸の返還を施すと、それぞれのヒストグラムはよく似た形であることが分かります。特に、短い時間足の2つの分布はほとんど重なって見えます。同じ分布からデータが生成されるという再生性を良く表した結果になっています。一方、1日足の分布は少しズレが顕著になっていて、より袖の広い分布へ変化してそうです。
になります。この横軸の返還を施すと、それぞれのヒストグラムはよく似た形であることが分かります。特に、短い時間足の2つの分布はほとんど重なって見えます。同じ分布からデータが生成されるという再生性を良く表した結果になっています。一方、1日足の分布は少しズレが顕著になっていて、より袖の広い分布へ変化してそうです。
仮に為替レートが確率的ボラティリティモデルで表せるとすると、どんなに秀逸な予測を行ったところで得られる損益の期待値は0です。手数料やスプレッド分だけ負けてしまいます。為替レートの生成過程の詳細は不明ですが、今回の観測からの個人的な感覚として、短時間(1時間以下程度)先の予測は殆ど不可能であろうと考えます。

コメント